
이진 트리의 탐색에는 크게 2가지 방법이 있다. 이번 포스팅에서는 깊이 우선 탐색(Depth-first Search)과 너비 우선 탐색(Breadth-first Search) 이 두 가지에 대하여 알아보고 각 순회들을 코드로 구현해 보려고 한다.
Depth-first Search(깊이 우선 탐색)
1. Pre-Order Traversal(전위 순회)
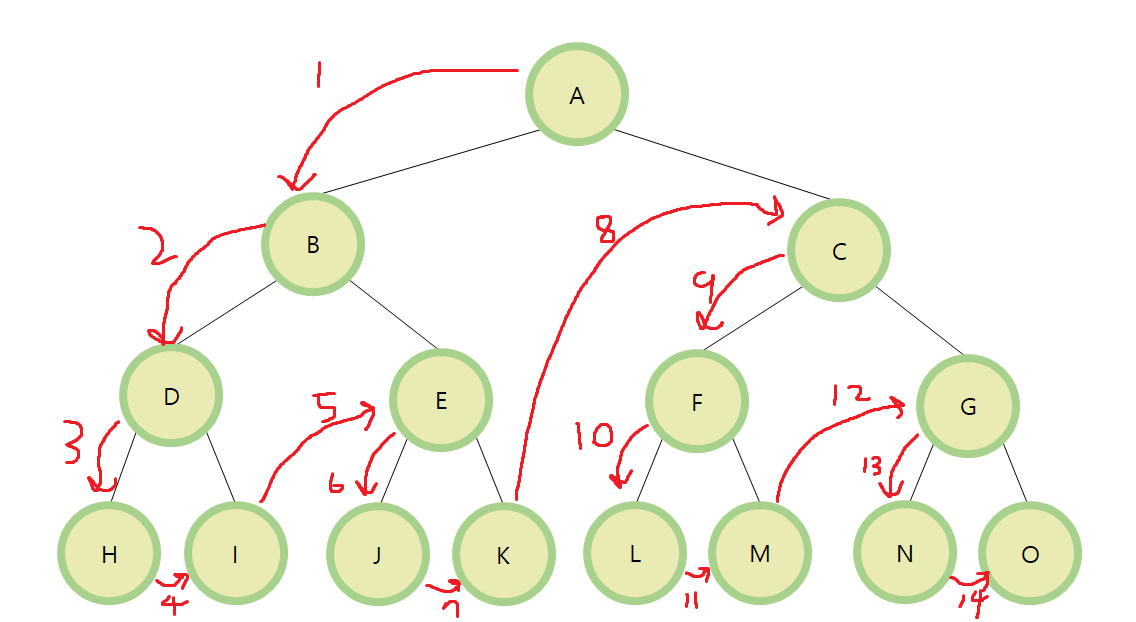
root -> left -> right
부모 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드
A, B, D, H, I, E, J, K, C, F, L, M, G, N, O 순으로 탐색
2. In-Order Traversal(중위 순회)
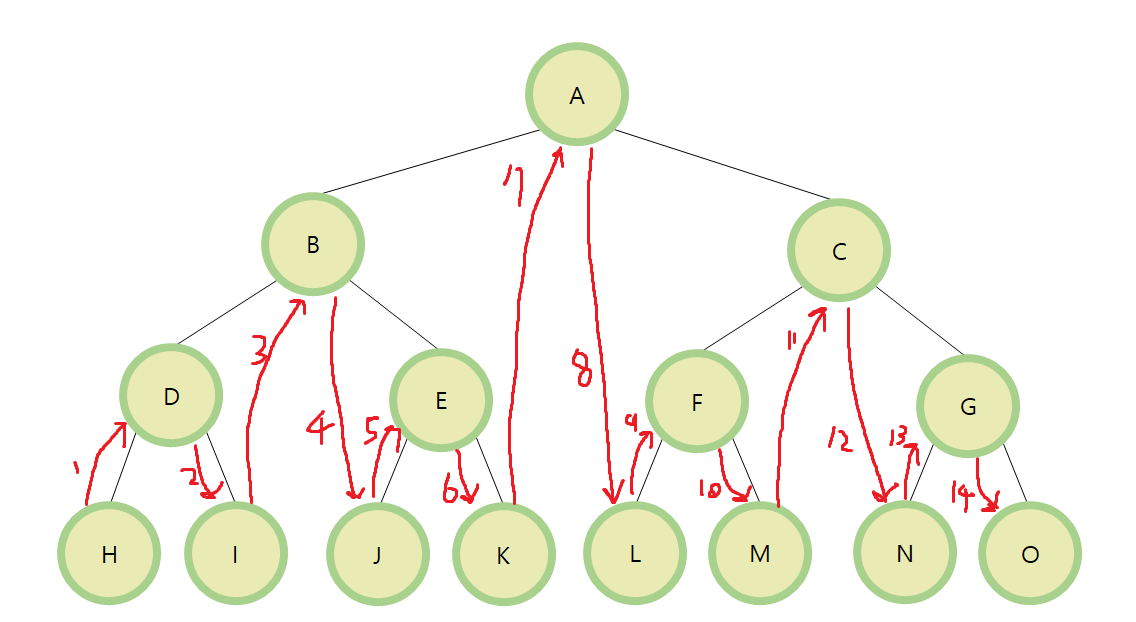
left -> root -> right
왼쪽 자식 노드 -> 부모 노드 -> 오른쪽 자식 노드
H, D, I, B, J, E, K, A, L, F, M, C, N, G, O 순으로 탐색
3. Post-Order Traversal(후위 순회)
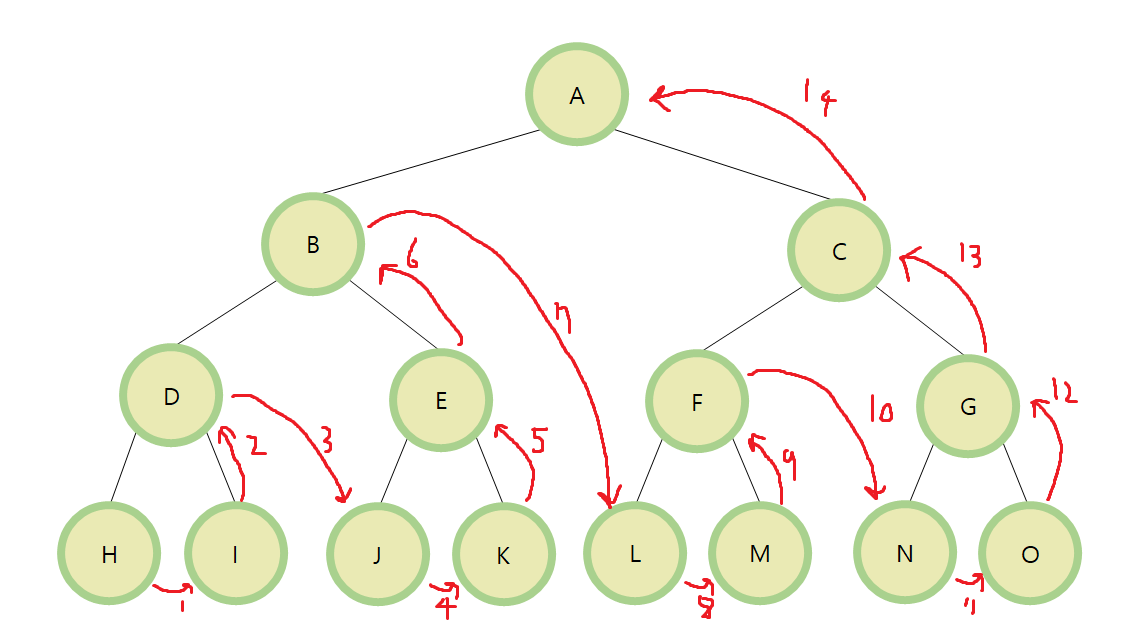
left -> right -> root
왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 부모 노드
H, I, D, J, K, E, B, L, M, F, N, O, G, C, A 순으로 탐색
Breadth-first Search(너비 우선 탐색)
너비 우선 탐색은 깊이 우선 탐색보다는 비교적 쉬운 탐색이다. 레벨 0부터 왼쪽 자식 노드 -> 오른쪽 자식 노드 순으로 탐색하면 된다.
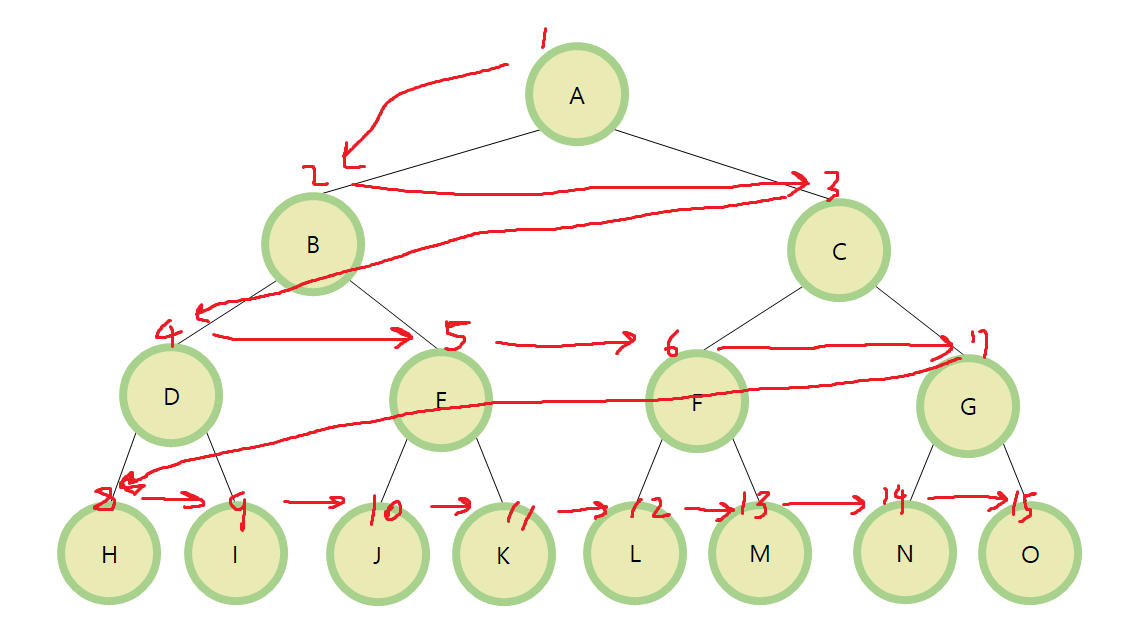
A, B, C, D, E, F, G, H, I, J, K, L, M, N, O 순으로 탐색
Javascript를 이용한 Depth-first Search(깊이 우선 탐색), Breadth-first Search(너비 우선 탐색) 구현
코드 전체
class treeNode {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
class bst {
constructor() {
this.root = null;
}
insert(data) {
let node = new treeNode(data);
// 루드가 설정되어 있지 않다면 루트를 node로 만들어 준다. node는 treeNode()에서 뼈대를 받아온다.
if(!this.root) {
this.root = node;
return this;
}
// 비교를 위해 current 를 설정해 준다.
let current = this.root;
// current가 true 라면 while문을 돌면서 data와 지금 현재 data인 current data를 비교한다.
while (current) {
// 중복된 값은 어떤 결과를 리턴하지 않는다.
if(data === current.data) {
return;
}
// data가 기준 data(current data) 보다 작다면 왼쪽에 넣어준다.
if(data < current.data) {
if(!current.left) {
current.left = node;
break;
}
// 이제 current data(기준)는 왼쪽의 data로 잡힌다.
current = current.left;
}
// data가 기준 data(current data) 보다 크다면 오른쪽에 넣어준다.
if(data > current.data) {
if(!current.right) {
current.right = node;
break;
}
// 이제 current data(기준)는 오른쪽 data로 잡힌다.
current = current.right;
}
}
}
// Breadth-first Search(너비 우선 탐색)
bfs() {
let node = this.root;
let queue = [node];
let finalData = [];
while(queue.length) {
node = queue.shift();
if(node.left) {
queue.push(node.left);
}
if(node.right) {
queue.push(node.right);
}
finalData.push(node.data);
}
return finalData;
}
// Depth-first Search(깊이 우선 탐색)
// 1. Pre-Order traversal(전위 순회)
preOrder() {
const finalData = [];
function traverse(node) {
finalData.push(node);
if(node.left) {
traverse(node.left);
}
if(node.right) {
traverse(node.right);
}
}
traverse(this.root);
return finalData;
}
// 2. In-Order traversal(중위 순회)
inOrder() {
let finalData = [];
function traverse(node) {
if(node.left) {
traverse(node.left);
finalData.push(node.data);
}
if(node.right) {
traverse(node.right);
}
}
traverse(this.root)
return finalData;
}
// 3. Post-Order traversal(후위 순회)
postOrder() {
let finalData = [];
function traverse(node) {
if(node.left) {
traverse(node.left);
}
if(node.right) {
traverse(node.right);
finalData.push(node);
}
}
traverse(this.root)
return finalData;
}
}
let nums = new bst();
nums.insert(10);
nums.insert(5);
nums.insert(11);
nums.insert(3);
nums.insert(6);
console.log(nums.bfs()); // 10, 5, 11, 3, 6
console.log(nums.preOrder()); // 10, 5, 3, 6, 11
console.log(nums.inOrder()); // 3, 5, 6, 10, 11
console.log(nums.postOrder()); // 3, 6, 5, 11, 10이진 탐색 트리 포스팅에서 구현해 놓은 코드에 아래 코드만 추가하여 코딩하였습니다.
탐색 별 도식화
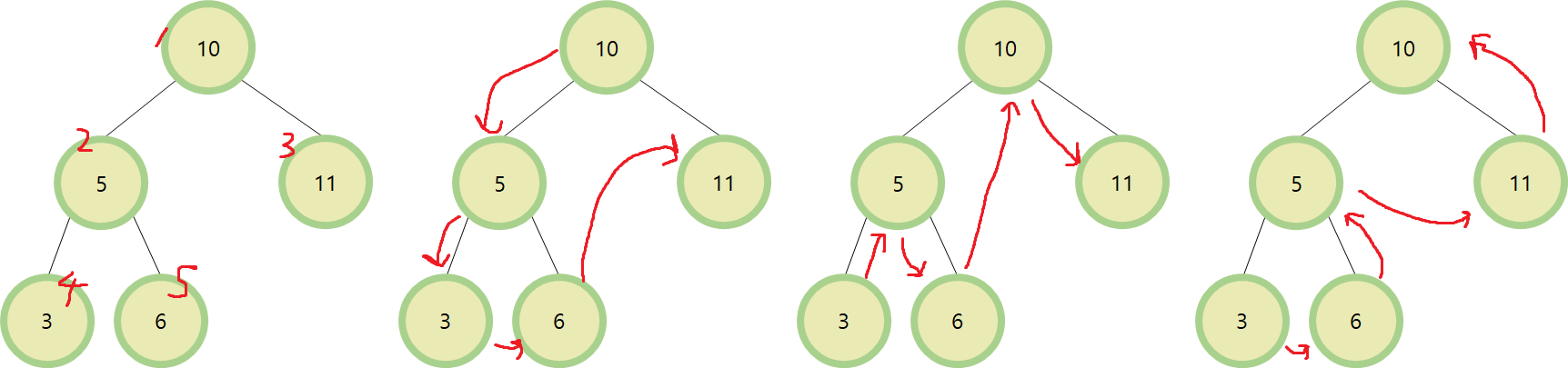
1. 너비 우선 탐색 : 10, 5, 11, 3, 6
2. 전위 순회 : 10, 5, 3, 6, 11
3. 중위 순회 : 3, 5, 6, 10, 11
4. 휘위 순회 : 3, 6, 5, 11, 10
'학습노트 > 자료구조' 카테고리의 다른 글
| [JavaScript] Quick Sort(퀵 정렬) (2) | 2020.09.03 |
|---|---|
| [JavaScript] Tree(트리) - Binary Search Tree(이진 탐색 트리) (0) | 2020.08.26 |
| [JavaScript] Tree(트리) - 이론학습 (0) | 2020.08.25 |
| [JavaScript] Queue - Linear Queue(선형 큐) (0) | 2020.08.25 |
| [JavaScript] Stack(스택) (0) | 2020.08.25 |





